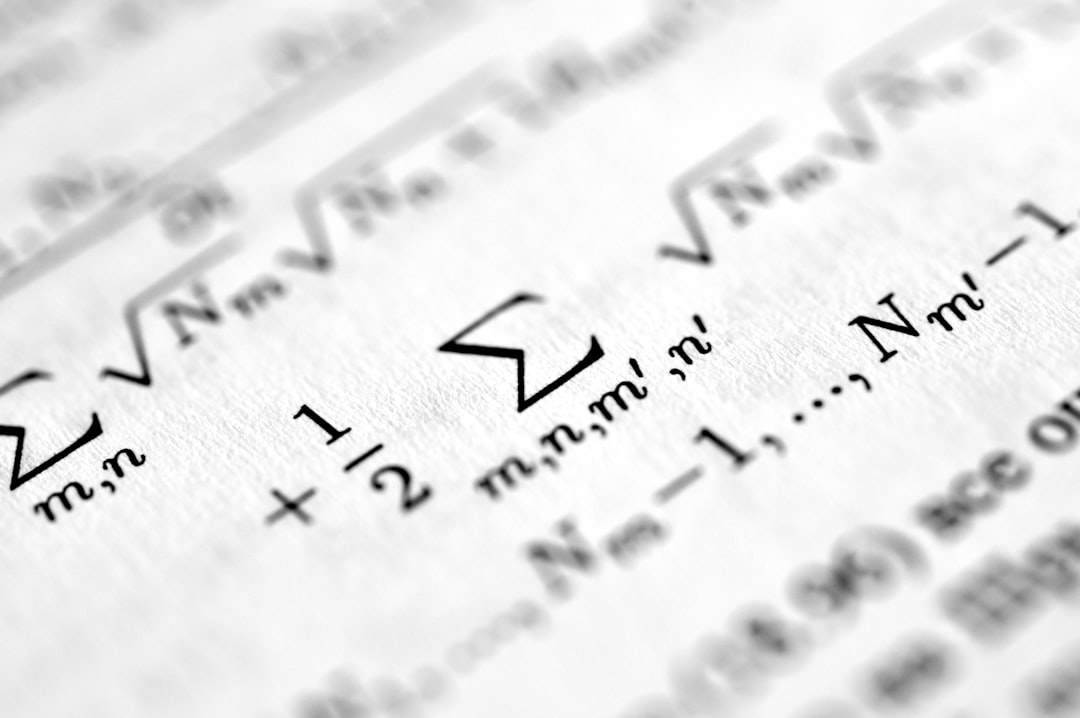Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Mathematical Interpretation of the Kubo Formula for Conductivity Analysis
The Kubo formula provides a mathematical lens through which we can understand electrical conductivity, especially in systems composed of non-interacting particles like electrons. It effectively quantifies the linear response of conductivity when an external electric field is applied, offering a way to analyze how materials react to such disturbances. Central to the formula's utility is its ability to bridge thermodynamic equilibrium states with the application of weak, oscillating electric fields. This linkage is particularly valuable when examining transport characteristics using time-correlation functions. Furthermore, the Kubo formula allows us to explore the intricate conductivity tensor, moving beyond simple averages to capture more comprehensive insights into the material's conductivity behavior. In essence, it offers a powerful framework for understanding how different materials conduct electricity, which is becoming increasingly important in computational frameworks, including those utilizing AI within structural analysis. The capacity to model and analyze complex conductivity responses in this manner offers opportunities to deepen our understanding of material performance under electrical stress.
The Kubo formula serves as a bridge between the microscopic quantum world of electrons and the macroscopic behavior we observe as electrical conductivity. It's rooted in the idea of how a system responds linearly to a small applied electric field, a concept central to understanding how materials behave under perturbations. The formula's derivation is firmly established within the quantum realm, focusing on spinless charged particles within a specific region. Notably, it only applies when those particles are in thermal equilibrium and subjected to a gentle, oscillating electric field.
Interestingly, the Kubo formula finds its place within Green-Kubo relations, where it helps us understand transport in terms of how fluctuations evolve over time. Through this, we can analyze the current generated in response to the applied field, providing a clear picture of the system's reaction within a defined spatial boundary.
From a mathematical viewpoint, the Kubo formula helps us calculate the current resulting from the electric field and then translates that into expressions for conductivity. It's not just about a single conductivity value, but rather, it enables the calculation of a complex conductivity tensor, allowing for a much richer understanding of how materials conduct electricity. This powerful formula, introduced in 1957, has become foundational in fields like condensed matter physics for gaining deeper insight into material conductivity. Its scope also extends to negatively charged systems in equilibrium, further expanding its relevance in the study of electrical conductivity. While the formula often deals with simplified particle interactions, it serves as a valuable tool to explore how a range of materials might behave in different circumstances.
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Quantum Mechanics Framework in Electrical Response Calculation
Within the realm of calculating electrical responses, the quantum mechanics framework provides a fundamental understanding of conductivity from a microscopic perspective. The Kubo formula is a cornerstone here, establishing a connection between the quantum mechanical behavior of charged particles and the macroscopic electrical conductivity. This framework highlights how a material's response to an external electric field is intrinsically linked to the quantum states of its constituent particles and the effects of scattering events which account for energy loss.
Moreover, this framework facilitates the integration of quantum concepts into classical models, such as the Drude model, where the interplay of parameters like electron density and mass are essential in defining conductivity. The quantum mechanical perspective is critical to expanding research efforts, particularly in understanding conductivity in new materials with complex electronic band structures, which contribute to unique transport characteristics.
The potential of this quantum framework lies in its ability to enrich our theoretical grasp of electrical conductivity, offering a pathway to enhance the capabilities of AI-driven structural analysis by providing a more robust and accurate understanding of how structures respond to electrical stimuli. However, the current research within this domain seems to still rely on the limitations of simplified particle interactions, which warrants further research efforts to achieve wider applicability.
The Kubo formula, while a powerful tool for understanding electrical conductivity within a quantum mechanical framework, often relies on simplifying assumptions. One such assumption is the presence of non-interacting particles. However, quantum mechanics tells us that interactions, especially in many-body systems, can be significant. Exploring the consequences of including such interactions – the so-called many-body effects – within the Kubo framework could offer new insights into how materials behave. For instance, understanding how electron-electron interactions impact conductivity is crucial for correctly predicting the electrical properties of materials. Additionally, the standard Kubo formula is often used under equilibrium conditions, whereas some applications demand an understanding of non-equilibrium behavior. Extensions to the formula can help capture these non-equilibrium dynamics which can be particularly important for understanding transient conductivity under rapidly varying electric fields, relevant in fields like ultrafast electronics.
Another aspect to consider is how temperature affects the conductivity predicted by the Kubo framework. As temperature changes, the scattering mechanisms influencing electron flow also change, impacting conductivity. This is why the formula often includes temperature dependence through terms like scattering times (τ). Some materials, classified as strongly correlated electron systems, deviate considerably from standard conductivity models due to the dominance of inter-electron interactions. The Kubo formula can be adapted to help shed light on the unusual conductivity responses observed in these materials, revealing phenomena such as non-linear conductivities.
Furthermore, the Kubo formula also allows us to study frequency-dependent conductivity. The response of a material to an applied electric field can be quite different at various frequency scales, which is of critical importance for high-frequency electronics and optics. It's notable that this formalism has played a crucial role in understanding specific quantum phenomena like the quantum Hall effect. In this intriguing quantum phenomenon, materials exhibit quantized Hall conductivity at very low temperatures, reflecting a link between the material's electronic band structure and its conductivity. Also, the influence of external magnetic fields can be incorporated into the Kubo formula. By considering the effect of the Lorentz force, one can better understand changes in conductivity resulting from magnetic fields, such as magnetoresistance.
Recent work has explored new geometric interpretations of the Kubo formula, connecting quantum mechanics to geometric phases in a novel way. This geometrical approach offers fresh insight into the behavior of materials in complex circumstances. It's worth noting that the quantum mechanical framework, as implemented through the Kubo formula, is increasingly important at smaller scales. The study of nanostructures, for instance, often reveals stark differences in conductivity compared to their bulk counterparts due to quantum confinement. This underscores the importance of a quantum mechanical framework for understanding conductivity in these emerging technologies.
While the Kubo formula represents a fundamental advancement in understanding electrical conductivity within a quantum framework, a lot remains to be uncovered, especially as it applies to non-equilibrium systems, many-body interactions, and novel materials. These areas warrant further investigation for us to gain a deeper and more accurate understanding of electrical conductivity.
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Machine Learning Integration with Band Structure Predictions
The integration of machine learning with band structure predictions represents a noteworthy development in computational materials science, especially within the context of electrical conductivity analysis. By merging density functional theory (DFT) with machine learning algorithms, researchers are capable of building predictive models that go beyond simply estimating band gaps to forecasting the complete k-resolved band structure of diverse materials. This approach significantly improves our ability to characterize the electronic properties of complex materials, such as spinel oxides, where the effective mass and the curvature of the band structure are crucial factors. Moreover, machine learning enables the exploration of previously unknown correlations, such as the impact of molecular substructures on conductivity, thus offering deeper insights for material design and performance optimization. While still in its development phase, this integration is expected to further enhance our comprehension of the connections between electronic properties and structural characteristics in novel materials. However, it is important to note that these models are only as good as the training data they are based on and there is potential for biases to influence their predictions. This integration of machine learning and band structure calculations is a powerful tool but requires careful interpretation and validation to provide reliable and unbiased insights into the nature of materials.
Machine learning (ML) has become increasingly integrated with density functional theory (DFT) to predict band structures, particularly for materials like spinel oxides. These ML-driven models are showing promise in accelerating the discovery of new materials by drastically reducing the computational time compared to traditional DFT methods. While DFT can be extremely accurate, it can be computationally intensive and slow, often requiring weeks or even months for complex systems. ML, on the other hand, has the potential to provide fast and accurate band structure predictions, enabling more rapid exploration of materials space.
One of the intriguing aspects of ML's application in this domain is its ability to find hidden correlations within band structures that traditional electronic structure methods might miss. This capability could potentially lead to the discovery of materials with completely novel electronic properties. It is also interesting that some ML models can achieve accuracy comparable to computationally intensive quantum mechanical calculations, but without requiring the same level of complexity. This makes them more practical and accessible for researchers and engineers in materials science.
ML models also open up the possibility of analyzing high-dimensional phase spaces, which can be challenging for traditional methods. This is particularly relevant for materials under extreme conditions like high pressure or temperature. However, a major hurdle in developing reliable ML models for band structure prediction is the need for high-quality training data. Using poorly curated datasets can lead to erroneous predictions. Therefore, there's a strong emphasis on collecting and utilizing robust, experimentally validated data in this area.
Beyond simply predicting band gaps, ML has expanded its scope to address other electronic properties, including effects like spin-orbit coupling and topological features. These properties are becoming increasingly critical in areas like quantum computing, highlighting the importance of incorporating them into material design workflows. Some ML approaches have started incorporating fundamental physical principles like symmetries and conservation laws directly into their algorithms. This helps improve predictive accuracy while ensuring the models adhere to the laws of physics.
The field is also witnessing ongoing research into hybrid models that combine the rigor of established electronic structure methods with the speed of ML. This fusion aims to create a balance between theoretical accuracy and computational efficiency. Such hybrid models hold the potential to reshape materials design pipelines, enabling researchers to quickly screen large numbers of candidate materials for various applications. For example, ML-powered band structure predictions can drastically expedite the search for optimal materials for semiconductor or superconductor applications.
Furthermore, the ability of ML to process massive datasets generated from experimental measurements and high-throughput computational studies can be instrumental in identifying patterns and trends in the electronic band structures of materials. Specifically, in complex alloy systems, ML can provide insights that lead to the synthesis of materials with precisely tuned electronic properties. In essence, it can guide the creation of materials with desired conductivity based on compositional variation.
While there is considerable enthusiasm surrounding ML's role in band structure prediction, it is important to acknowledge the limitations. Understanding how these models deal with phenomena outside their training data remains a challenge. Continued research is crucial to push the boundaries of ML in this field, especially for exploring unconventional materials and situations where current models may falter.
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Temperature Effects on Electronic Transport Properties
Temperature plays a crucial role in shaping the electronic transport properties of materials, particularly their electrical conductivity. At low temperatures, unique phenomena like the Kondo effect can emerge, impacting how electrons scatter, as observed in certain thin film materials. For instance, the magnetic moments of electrons in La1-xPrxNiO3 thin films contribute to altered conductivity at low temperatures. In contrast, at more typical temperatures like room temperature, electron interactions with lattice vibrations (phonons) become the dominant factor, governing electron scattering and heat transfer, primarily within metallic materials.
Interestingly, as temperatures rise, electrical conductivity generally increases. This behavior is driven by the thermal excitation of charge carriers (electrons and holes), leading to a revised understanding of what constitutes an insulator. Moreover, computational approaches based on fundamental principles are helping us unravel the intricate link between temperature changes and electronic transport properties. These methods provide a detailed understanding of how temperature affects conductivity in a wide range of materials, including those with promising thermoelectric properties, such as Mg3Sb2. Understanding these temperature effects is crucial for a comprehensive view of a material's electrical response and is especially important when considering the application of these materials in a variety of technologies. While we've made progress in understanding these relationships, the field is still evolving, and continued exploration will undoubtedly reveal further intricacies in how temperature shapes the electronic transport properties of materials.
The influence of temperature on the electronic transport properties of materials is a multifaceted and fascinating area of study. For instance, in intrinsic semiconductors, we see a direct relationship between temperature and conductivity. As temperature rises, more electrons gain enough energy to jump into the conduction band, increasing the number of charge carriers and, consequently, conductivity. However, in heavily doped semiconductors, this relationship isn't so straightforward. While higher temperatures might generate more charge carriers, they also increase scattering events, effectively reducing carrier mobility. This interplay between thermal energy and charge transport leads to a more nuanced temperature dependence of conductivity.
Interestingly, some materials exhibit a transition from metallic behavior to an insulating state with temperature fluctuations. This phenomenon, often termed a Mott transition, arises from how thermal excitation can cause localized electrons to vacate their states. Consequently, the overall electronic structure changes, significantly affecting the material's ability to conduct electricity.
At extremely low temperatures, we encounter a different set of phenomena where quantum effects start to dominate. Traditional scattering events, like those caused by phonon interactions, become less important, allowing quantum properties like electron coherence to take center stage. This can manifest as rather unusual conductivity behaviors, such as the remarkable phenomenon of zero electrical resistance in certain superconducting materials.
Another intriguing aspect is the occurrence of negative differential conductivity (NDC) in certain materials as temperature changes, specifically under high electric field conditions. This counterintuitive response can be valuable in designing electronic devices like oscillators and amplifiers.
Many materials display a temperature-dependent conductivity that follows an Arrhenius-like equation. This "thermal activation" behavior suggests that thermal energy directly affects the ability of charge carriers to overcome activation energy barriers, influencing their overall mobility.
Understanding how temperature affects various scattering mechanisms is crucial for predicting a material's response to different thermal conditions. Temperature changes influence the interactions between charge carriers and other components of the material, like ionized impurities, acoustic phonons, and optical phonons. Each type of scattering event plays a distinct role in shaping the conductivity behavior.
In materials where multiple charge carriers, such as electrons and holes, are present, changes in temperature can affect each type of carrier differently. This creates a two-component conductivity model that necessitates a more detailed understanding of charge transport.
The arrangement of atoms in crystalline solids can also lead to a temperature-induced anisotropy in electrical conductivity. Different crystallographic directions can have unique conductivity characteristics because of the unique interactions between charge carriers and the thermal vibrations within the crystal lattice.
The influence of temperature on the frequency-dependent conductivity can affect high-speed electronics. At higher temperatures, carrier dynamics can become faster, impacting the speed and integrity of signals in advanced devices.
Finally, near phase transitions in materials like ferroelectrics and magnets, the conductivity can display temperature-dependent fluctuations. These critical fluctuations, which become increasingly significant as the material nears its critical point, can cause dramatic changes in the material's properties, impacting the design of electrical systems.
It's clear that temperature plays a crucial and multifaceted role in the electronic transport properties of materials. Understanding these complex relationships is becoming increasingly critical as we develop new materials and devices for a wide array of applications. Further exploration and a deeper understanding of these temperature-related effects will likely continue to reveal novel phenomena and potential applications.
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Structural Analysis through 3D Microstructure Mapping
3D microstructure mapping has become increasingly important in understanding how the internal structure of materials impacts their overall properties. This is especially true for materials used in applications like batteries and fuel cells, where the performance hinges on how ions and electrons move through complex internal networks. Using advanced imaging tools, we can create 3D representations of these structures, allowing researchers to see the intricate details that influence electrical conductivity and the paths ions take through the material. Combining this detailed mapping with powerful computational methods, including machine learning, allows for more sophisticated analysis. We can now extract key information about the interactions between different components within a material. This enhanced understanding leads to improved design principles, enabling the development of better batteries, fuel cells, and other energy technologies. The fusion of 3D microstructure mapping and AI-powered simulations is a growing field, promising to fundamentally change the way we design and optimize materials in the energy sector and beyond. While this approach provides significant advancements, the field is still under development and there are still limitations in accurately capturing the full complexity of many materials, which highlights opportunities for future research.
Three-dimensional reconstructions of materials, like those used in battery studies, allow for high-resolution imaging and computational analysis, leading to a better grasp of material properties. Machine learning methods have shown promise in extracting statistical information about physical contact within battery systems, specifically between active particles and the conductive matrix. This type of analysis is useful for understanding how these materials conduct electricity. Calculating the effective conductivity and paths of ionic conduction relies on local conductivity values and corresponding electrical potentials in the structure.
The microstructure of battery electrodes is crucial for optimizing performance at the cell level. Computational design methods that use generative AI are being explored to enhance the manufacturing process by improving electrode properties. The performance of energy devices, like batteries and fuel cells, is strongly affected by the electrode's microstructure, prompting a need for simulations to optimize design. Digital twin simulations have shown that electrodes made with certain polymer composites have better characteristics like increased volume fraction, lower tortuosity, and larger contact area when compared to less optimized materials.
A 3D microstructure model derived from X-ray nanocomputed tomography reveals detailed aspects of the carbon-binder domain in lithium-ion battery electrodes. Conductivity modeling has shown that in certain conductivity ranges, the conductivity in the through-thickness direction at the yarn interface is notably increased (by 354%).
This type of 3D mapping of microstructures provides a pathway to gain insights into the relationships between the structure and mechanical properties of advanced materials. Modeling the microstructure can shed light on the electrical and ionic conduction structures within solid electrolyte materials, which is particularly useful in the optimization of all-solid-state battery technology.
It's interesting how these techniques allow researchers to examine a wide range of length scales, from the very small to the macroscopic. However, I remain curious about the assumptions made in translating the detailed microstructural features to macroscopic conductivity. We need to be critical of the assumptions in these modeling approaches, as sometimes, the complexity of the material's interactions can't be captured within the simplified models. While exciting, these methods are still developing and require careful validation, especially as we apply them to new materials and operating conditions.
Understanding the Formula for Electrical Conductivity in AI-Driven Structural Analysis A Mathematical Framework - Non Linear Response Patterns in Advanced Material Systems
Advanced materials often display complex and non-proportional responses to external stimuli, a phenomenon that conventional linear models, often based on the Kubo formula, struggle to capture. These nonlinear response patterns are especially prominent under demanding conditions such as large deformations, structural failure, or complex loading scenarios. In such situations, the assumption of a linear relationship between applied force or field and the resulting material response breaks down. Consequently, more sophisticated analytical tools are needed. Examples of such tools include nonlinear frequency response analysis and methods capable of describing the intricacies of phenomena like optical conductivity. Materials that exhibit nonlinear behavior are commonly encountered in a broad range of applications, from structural engineering to energy production, highlighting the need for deeper investigations to fully understand and optimize the performance of these materials. The field of nonlinear material response is a vibrant one that calls for ongoing research and innovative model development to better understand the rich behavior of advanced material systems. It's a reminder that the world of materials is often far more complex than simple linear relationships can encompass.
The Kubo formula, while a powerful tool, primarily captures linear conductivity responses, meaning it assumes a direct proportionality between the applied electric field and the resulting current density. However, many advanced material systems exhibit more complex, nonlinear response patterns. These deviations from linearity become particularly apparent under high electric fields or extreme temperatures. For instance, we might observe unexpected changes in conductivity that don't align with the conventional linear predictions.
The relationship between conductivity and the frequency of an applied electric field, or equivalently, the wavelength, is another area where nonlinear behavior can emerge. In high-speed electronic applications, this frequency-dependent response becomes crucial as materials can behave drastically differently at various frequencies. This emphasizes the need for models that capture the intricate interactions between electric fields and materials at various frequency ranges.
Adding another layer of complexity is the presence of "memory effects" in some advanced materials. This means that the material's previous electrical history can influence its subsequent response to an identical electric field. This phenomenon, which has links to areas like neuromorphic computing, challenges our traditional understanding of conductivity, requiring us to develop sophisticated models that incorporate these memory elements.
We also find that the presence of structural defects or disorder within a material's structure can drastically alter the conductivity response, often in nonlinear ways. These defects can create localized states within the material, influencing how charge carriers move through the system. The resulting conductivity behavior can differ considerably from predictions based on idealized, perfect crystalline structures.
Some materials exhibit magnetoresistance, where applying a magnetic field leads to nonlinear changes in conductivity. These effects, vital for applications in sensors and storage devices, add another dimension to the complexity of predicting electrical responses.
When materials possess multiple types of charge carriers, such as electrons and holes, their interactions can lead to nonlinearities. The competition and interplay between these carriers can lead to unexpected changes in overall conductivity, especially in heterostructures and alloys.
Furthermore, some systems display nonlinear electrical damping, where energy loss due to interactions between charged particles and lattice vibrations (phonons) becomes a factor. These damping effects aren't captured by simpler linear models and can significantly alter the overall material response.
The response of advanced materials can also change over time, creating dynamic variations in their electrical conductivity. This temporal dependency highlights the importance of models that capture transient conductivity responses to rapid changes in external stimuli.
Nonlinear transport phenomena can also become crucial in complex microstructures, especially when we consider the pathways available for ionic movement. For example, an increase in connectivity within a porous medium can lead to unexpected increases in ionic conductivity, challenging traditional models based on simple conductivity calculations.
Finally, the field of high-temperature superconductivity presents intriguing cases of nonlinear responses. In some materials, a gradual increase in conductivity can suddenly lead to a state of zero electrical resistance. Understanding these nonlinearities is essential for improving our capabilities to engineer and optimize superconducting materials and technologies.
In summary, understanding nonlinear response patterns in advanced materials is crucial for the continued development of technologies relying on precise control of electrical conductivity. While linear models offer valuable initial insights, developing more sophisticated models that accurately capture these nonlinear effects is essential for maximizing the performance of future devices. The intricate interplay between charge carriers, defects, external fields, and material geometry requires a deeper understanding of these complex systems, which presents exciting challenges and opportunities for future research.
More Posts from aistructuralreview.com:
- →How Frontier's Denver-Portland Route Became a Key Testing Ground for Ultra-Low-Cost Carrier Operations in 2024
- →JetBlue's Aircraft Fleet Modernization Impact on 2024 Black Friday Route Expansion
- →NX Assembly Load Options 7 Critical Settings for Precise Part Loading in Manufacturing Environments
- →Understanding Coulomb's Law A Step-by-Step Guide to Electric Field Calculations in Structural Analysis
- →Optimizing Antimatter Production A Technical Analysis of Supercritical Phase Shifter Power Requirements in AI-Driven Systems
- →Analyzing K Values A Comprehensive Guide to Pressure Loss Coefficients in Pipe Fittings